Introduction
The binary number is the carrying of the carrying, 0, 1 is the basic operator; the computer operator is used in binary. The basis of the computer is binary. Commonly designed in early design is mainly decimal (because we have ten fingers, it is more reasonable choice, and the finger can represent ten numbers. 0 The concept is until it will appear for a long time, so it is 1-10 Not 0-9). After the electronic computer appears, the use of tubes is used to indicate that ten states are too complicated, so there are only two basic states, open and off. That is, the two states of the tube determine the use of binary using binary based electronic computers.
binary count
four operation
plus calculation: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10, all 2 into 1;
minus operation: 1-1 = 0, 1-0 = 1, 0-0 = 0, 0-1 = 1, to the high position 1 when 2; < / p>
multiply: 0 × 0 = 0, 0 × 1 = 0, 1 × 0 = 0, 1 × 1 = 1, only the result is "1" when it is "1";
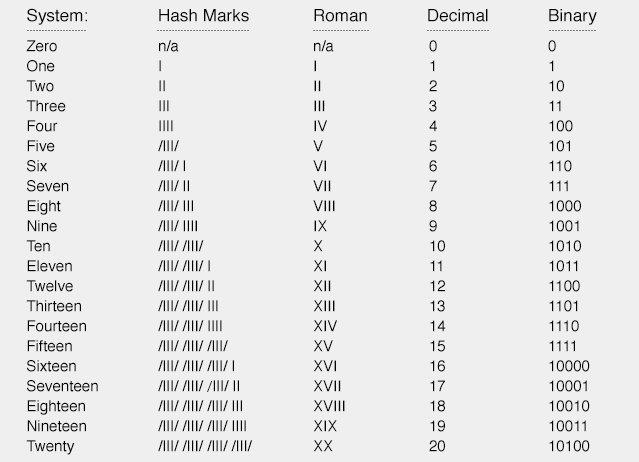
In addition to operation: The number of binary numbers is only two numbers 0, 1, so its merchants are 1 or 0.
logic operation
In order to perform various processing of binary information, the logical algebra is needed. There are three most basic logical operations in logical algex: logical plus (also known as "or" operation, with symbol "or", "or" + "), logic multiplied (also known as", using symbol " And "," ∧ "or" · "indicated), and inverse (also known as" non "operation, expressed as the symbol" not "or" - "), indicating that the following:
logic plus: 0 ∨0 = 00 ∨1 = 11∨0 = 11∨1 = 1
logic multiplied: 0 ∧ 0 = 00 ∧1 = 01 ∧0 = 01 ∧1 = 1
Logic is not: "0" is "1", "1" is "0" after reflecting.
Differential characteristics
1, if a value of a binary (integer) number is 1, then this number is odd; if this bit is 0, Then this number is even.
2, if a low-end N bit of a binary number is zero, then this number can be divided by 2n.
3, if a binary number of Number is one, while others are zero, then this number is equal to.
4, the result of all bit left shift positions in a binary number is multiplied by two.
5, the result of one bit of all bit-free binary numbers is equivalent to the number in addition to two (this pair of symbols is not applicable).
6, reverse all bits of a binary number (that is, all one change to zero, all zero change to one) is equivalent to handle the number (change the symbol) minus one.
7, the maximum number of non-symbolic binary numbers indicated by any given number is always zero.
8, the result of zero decrementing (reduced) is always a maximum number of no symbolic binary numbers represented by a given number.
