Problem Introduction
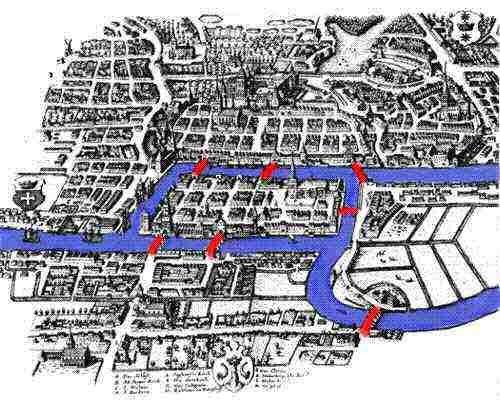
18th centuries of the Gobini, there is a river through, there are two islands, there are Seven bridges link two islands with the river bank (such as outline map). Some people have proposed a question: How can a pedestrian do not repeat, do not miss the seven bridges at a time, and finally return to the starting point. Later, large mathematician Euli transformed it into a geometric issue - a painting problem. He not only solved this problem, but also gives a fill of a chart of a picture: The number of odd points is not 0 is 2 (even the number of odd numbers, "if it is The even number is called even. If you want to draw a picture, you must have an even thing in the middle, that is, there is another way to have another way, and the singularity may only be on both ends, so any figure can be drawn, Did you have or on both ends).
Inference method
When the Euler visited Prussian Gobisburg (now Russia Galoningrad), he found a very interesting local public. Confuciate. There is a river called Pregel in Gobinic City, this interesting pastime is a walk from all seven bridges in Saturday, and each bridge can only pass once and the starting point must be the same place. .
Euchi puts each piece into a point, connecting two terrestrial bridges.
It is impossible to inquire such a way. His argument is this, except for the starting point, each time a person enters an land (or point) by a bridge, he (or her) will also leave this point by another bridge. Therefore, each line is at a point, two bridges (or lines) are calculated from the line from the start point and the line of the last return point, so the number of bridges connected to other land is almost even.
There is a problem
Seven bridge, there is no point containing the number of orientations, so the above tasks cannot be completed.
Euler is very important, it is also very clever, it is demonstrating the uniqueness of mathematician dealing with practical problems - abstracts an actual problem into a suitable "mathematical model". This research method is "Mathematical Model Method". This doesn't need to use how deep theory, but think of this, but the key to solve the problem.
Next, Euler uses a painting in the figure to judge the guidelines, and quickly judges that the 7 bridges that do not repeat the port of Doinsburg once. In other words, how many years come, people pay attention to the non-repetitive route, do not exist at all. A problem that has been difficult to live, is actually such a spare answer!
Final achievement
The initial period of the problem
After the question is raised, many people are very interested in this, but they are experimenting, but In a long time, I have never been resolved. With ordinary mathematical knowledge, each bridge is taken once, and the seven bridges all walk a total of 5040, and so many cases, it will be trial, which will be a lot of workload. But how can I find a route that successfully walks through each bridge instead of repeating? Therefore, a famous "Gossoburg Seven Bridge Problem" is formed.
Problem Post-exposure
1735, there are several college students write a letter to the genius mathematician Eura, who is working at Russia, the Porsopian Academy of Sciences. Ask him to help solve this problem. Ou was observing the Hard Bridge in the Gobi, earnestly thinking about it, but he had not been able to succeed, so he suspected that the Qiqiao question did not solve it?
In 1736, after a year of research, 29-year-old Orap submitted the "Gobi Seven Bridge" papers, successfully solved this problem, and creating a new branch of mathematics - --Graph Theory.
In the paper, Eutu will abstract the Qiqiao issue and take each piece into a point, connect two land bridges. And thereby got the same geometry as shown. If we use A, B, C, D four points to represent the four areas of Gobinic. Such a famous "seven bridge problem" is converted to whether it is possible to use a non-repetitive painting of the seven lines. If you can draw, you must have end points and starting points in the graphics, and the starting point and end point should be the same. Since the symmetry can be seen from B or C as the starting point, if it is assumed that A is the starting point and end point, then There must be one away from the wire and the corresponding entry line. If we define the number of rows of the line entering A, the number of rows that leave the wire is exit, and the number of rods of the line is a degree of A, then a The degree and the degree of degrees are equal, that is, the degree of A should be an even number. That is, it is necessary to make a decisor from A. The degility of the degility should be an even number, and the degree of actually A is 5 is odd, so it can be seen that it is unsubable from A. At the same time, if it is from B or D, since B, D's degrees are 3, 3, each is odd, that is, the starting point is unpublished.
It is known that the above reason is that the abstract mathematical problem is unsubalypted, ie "seven bridge problems" is also unpublished.
From this we get: Euler loop relationship
So we can know that A graphics can be drawn, must meet the following two conditions:
1. Graphics must be connected.
2. The number of "odds" in the figure is 0 or 2.
We can also verify that the graphics can be drawn. It can also be judged to judge the "seven bridge problems", 4 points are odd, can know that the picture cannot be "drawn", that is, there is no repeatedly pass all seven bridges.
In 1736, Eucula explained his solving method in the Papers of the "Gobinburg 7 Bridge", which was handed over to the Petersburg Academy. His induction, laying the foundation for the new mathematical branch - the establishment of topology.
Qiqiao Question and Euler Theorem
Euler adopts the research on the Qiqiao issue, not only to replunate the problem proposed by Gobinburg residents And got and proved three conclusions related to a stroke, and people are often called the Euler theorem. For a connecting map, it is usually called Euler Road from a route that is drawn from a node. People usually call a pair of Euler circuits that are drawn back to the starting point. A picture with the European loop is called the Euler map.
This topic is included in the 12th book of the Mathematics Mathematics. 104 pages.
This topic is also included in the first volume of the first volume. On page 121.
A painting
⒈⒈⒈ ⒈ 通 通 通 图 图 图 图 图 图 图 图 图 图 图 通 图 图 图 图 图 图 图When you draw, you can take anything at the starting point, and finally you can draw this picture with this point.
⒉ Where only two odd perspective (the rest is even), it must be drawn. When you draw, you must put a strange point as the starting point, and another odd point is end.
⒊ Other status maps cannot draw. (The number of odd points can be calculated in the second figure to draw a few pieces.)
