Historical background
More than half a century before Maxwell was born, humans have made great progress in understanding electromagnetic phenomena. In 1785, the French physicist C. A. Coulomb (Charles A. Coulomb) established Coulomb's law describing the interaction force between two point charges on the basis of the results of the torsion balance experiment. In 1820, H. C. Oersted (Hans Christian Oersted) discovered that electric current can deflect magnetic needles, thereby linking electricity with magnetism. Afterwards, A. M. Ampère (Andre Marie Ampère) studied the interaction between electric currents and put forward many important concepts and the law of Ampere’s loop. M. Faraday (Michael Faraday) has made outstanding contributions in many aspects, especially the law of electromagnetic induction published in 1831, which is an important theoretical basis for motors, transformers and other equipment.
In 1845, the three most basic experimental laws on electromagnetic phenomena: Coulomb's law (1785), Biot-Savart law (1820), Faraday's law of electromagnetic induction (1831 ~ 1845) ) Has been summed up, Faraday’s concepts of "line of force" and "line of magnetic force" (now also called "line of electric field" and "line of magnetic force") have been developed into the "concept of electromagnetic field." From 1855 to 1865, Maxwell comprehensively reviewed Coulomb's law, Biot-Savart's law and Faraday's law, and brought mathematical analysis methods into the field of electromagnetic research, which led to the birth of Maxwell's electromagnetic theory. .
Before Maxwell, all theories on electromagnetic phenomena were based on the concept of over-distance action. It was believed that the interaction between charged bodies, magnetized bodies, or current-carrying conductors could be carried out directly beyond the intermediate medium. And it is done immediately, that is, the propagation speed of electromagnetic disturbance is considered infinite. At that time, only Faraday had different opinions. He believes that the above-mentioned interactions are related to intermediate media and are carried out through the transfer of intermediate media, that is, advocating the theory of indirect transfer.
Maxwell inherited Faraday’s point of view, referred to the model of fluid mechanics, applied rigorous mathematical forms to summarize the work of the predecessors, proposed the hypothesis of displacement current, extended the meaning of current, and concluded the basic laws of electromagnetic field There are four differential equations, which are the famous Maxwell equations. He analyzed this set of equations, foreseeing the existence of electromagnetic waves, and concluded that the propagation speed of electromagnetic waves is a finite value (close to the speed of light), and that light is also an electromagnetic wave of a certain frequency. He wrote all of the above in his paper entitled "On Electricity and Magnetism".
In 1887, Heinrich R. Hertz used experimental methods to generate and detect electromagnetic waves, which confirmed Maxwell’s foresight. Between 1905 and 1915, Albert Einstein's theory of relativity further demonstrated the relationship between time, space, mass, energy, and motion, indicating that electromagnetic fields are a form of matter, and the theory of indirection has been recognized.
Equation composition
Maxwell’s equations are composed of four equations:
Gauss’s law: This law describes the relationship between electric field and charge distribution in space . The electric field lines start with a positive charge and end at a negative charge (or infinity). Calculate the number of electric field lines passing through a given closed surface, that is, its electric flux, and you can know the total charge contained in this closed surface. In more detail, this law describes the relationship between the electric flux passing through an arbitrary closed surface and the charge in the closed surface.
Gaussian magnetic law: This law shows that magnetic monopoles do not actually exist. Therefore, there is no isolated magnetic charge, and the magnetic field line has no initial point and no end point. The magnetic field lines will loop or extend to infinity. In other words, magnetic field lines entering any area must leave that area. In terminology, the magnetic flux passing through any closed surface is equal to zero, or the magnetic field is a passive field.
Faraday's law of induction: This law describes how a time-varying magnetic field induces an electric field. Electromagnetic induction is the theoretical basis for the manufacture of many generators. For example, a rotating bar magnet generates a time-varying magnetic field, which in turn generates an electric field, causing the adjacent closed circuit to induce current.
Maxwell-Ampere's law: This law states that a magnetic field can be generated in two ways: one is by conducting current (the original Ampere's law), and the other is by time-varying electric field, or displacement Current (Maxwell's correction term).
In electromagnetics, Maxwell's correction term means that a time-varying electric field can generate a magnetic field, and because of Faraday's law of induction, a time-varying magnetic field can generate an electric field. In this way, the two equations theoretically allow self-sustaining electromagnetic waves to propagate in space.
The main points of Maxwell’s electromagnetic field theory can be summarized as follows:
①Several discrete charged objects or currents, all electrical and magnetic interactions between them are passed between them What is transmitted in the middle area, regardless of whether the middle area is a vacuum or a physical substance.
②Electric energy or magnetic energy not only exists in charged bodies, magnetized bodies, or charged objects, but most of it is distributed in the surrounding electromagnetic field.
③If there is an interruption in the circuit formed by the conductor, the conduction current in the circuit will be compensated through by the displacement current in the dielectric, that is, the full current is continuous. And the relationship between the displacement current and the magnetic field it generates is the same as that of the conduction current.
④ The magnetic flux has neither a beginning nor an end, that is, there is no magnetic charge.
⑤Light waves are also electromagnetic waves.
There are two ways to express Maxwell’s equations.
1. The integral form of Maxwell's equations is a mathematical model that describes the electromagnetic field in a certain volume or area. The expression is:
Equation ① is the law of total current derived from the generalization of the law of Ampere’s loop, and its meaning is: the line integral of the magnetic field intensity H along any closed curve is equal to the area passing through the limited area of this curve Full current. The first term on the right side of the equal sign is the conduction current. The second term is the displacement current. Equation ② is the expression of Faraday's law of electromagnetic induction, which shows that the line integral of the electric field intensity E along any closed curve is equal to the negative value of the rate of change of the magnetic flux passing through the area defined by the curve with respect to time. The closed curve mentioned here does not necessarily have to be composed of conductors, it can be a dielectric loop, or even just any closed contour. Equation ③ represents the principle of magnetic flux continuity, indicating that for any closed curved surface, as much magnetic flux enters the curved surface, the same amount of magnetic flux leaves. That is to say, the B line has neither a beginning nor a terminal; it also shows that there is no magnetic charge corresponding to the electric charge. Equation ④ is the expression of Gauss's law, which shows that under time-varying conditions, the net flux of D from any closed surface should be equal to the sum of all free charges in the volume enclosed by the closed surface.
2. Maxwell's equations in differential form. The differential form of Maxwell's equations is for every point in the field. Using the del operator, they can be written as
Equation ⑤ is the differential form of the law of total current, which shows that the curl of the magnetic field intensity H is equal to the total current density at this point (conduction current density J and displacement current density The sum), that is, the vortex source of the magnetic field is the full current density, and the displacement current can generate the magnetic field just like the conduction current. Formula ⑥ is the differential form of Faraday's law of electromagnetic induction, which shows that the curl of the electric field intensity E is equal to the negative value of the time rate of change of the magnetic flux density B at this point, that is, the vortex source of the electric field is the time rate of change of the magnetic flux density. Equation ⑦ is the differential form of the principle of magnetic flux continuity, which shows that the divergence of the magnetic flux density B is always equal to zero, that is, the B line has no beginning and no end. That is to say, there is no magnetic charge corresponding to the electric charge. Equation ⑧ is a generalization of Gauss's law of electrostatic field, that is, under time-varying conditions, the divergence of electric displacement D is still equal to the free charge density at this point.
In addition to the above four equations, the constitutive relationship of the medium is required
to finally solve the problem of solving the field quantity. Where ε is the dielectric constant of the medium, μ is the permeability of the medium, and σ is the conductivity of the medium.
Expression form
Integral form
The integral form of Maxwell’s equations is as follows:
This is 1873 Around the year, Maxwell proposed four equations expressing the universal law of electromagnetic fields. Among them:
(1) describes the nature of the electric field. In general, the electric field can be an electric field of free charge or an induced electric field excited by a changing magnetic field, and the induced electric field is a vortex field, and its electric displacement line is closed and does not contribute to the flux of a closed curved surface.
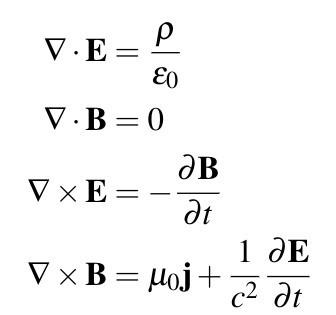
(2) describes the nature of the magnetic field. The magnetic field can be excited by the conduction current or the displacement current of the changing electric field. Their magnetic fields are all vortex fields, and the magnetic induction lines are closed lines, which do not contribute to the flux of the closed curved surface.
(3) describes the law of the changing magnetic field to excite the electric field.
(4) describes the law of conducting current and changing electric field to excite magnetic field.
Form in the steady field
When
, the equations are reduced to the equations of the electrostatic field and the steady magnetic field :
Form in free space without field source
When, the equation system becomes the following form:
The integral form of Maxwell's equations reflects the relationship between the amount of electromagnetic field (D, E, B, H) and the field source (charge q, current I) in a certain area of space.
Differential form
In the actual application of electromagnetic field, it is often necessary to know the relationship between the amount of electromagnetic field point by point in space and the charge and current. From the mathematical form, the integral form of Maxwell's equations is transformed into a differential form. The inverted triangle is the Hamiltonian.
Note:
(1) In different inertial reference frames, Maxwell's equations have the same form.
(2) To apply Maxwell's equations to solve practical problems, the influence of the medium on the electromagnetic field must also be considered. For example, in a uniform and isotropic medium, the amount of electromagnetic field has the following relationship with the characteristics of the medium:
In a non-uniform medium, the boundary value of the amount of electromagnetic field on the interface should also be considered Relationship. Using the initial value condition of the field quantity when t=0, in principle, the electromagnetic field at any point in space at any time can be obtained, namely E(x, y, z, t) and B(x, y, z, t).
The following is the Maxwell equations under the Gauss unit system
Physical property equations
When there is a medium, due to electric and magnetic fields The interaction with the medium makes the amount of electromagnetic field related to the characteristics of the medium. Therefore, the above-mentioned Maxwell equations are not complete at this time, and the physical property equations describing the properties of the medium (isotropic medium) need to be supplemented, respectively
In the formula, ε, μ and σ are the absolute dielectric constant, absolute permeability and conductivity of the conductor, respectively Rate.
Further theoretical proof that Maxwell's equations and physical property equations together are a complete set of equations for determining the changes of electromagnetic field. That is to say, when the charge and current are given, the change of the electromagnetic field can be completely determined from the above equation according to the initial conditions (and necessary boundary conditions). Of course, if you want to discuss the effect of the electromagnetic field on the charged particles and the movement of the charged particles in the electromagnetic field, you also need the Lorentz force formula.
Complex number form
For sinusoidal time-varying fields, complex vectors can be used to express the law of electromagnetic fields as complex numbers.
In the complex electromagnetic field law, since the complex field quantity and the source quantity are only functions of space position, when solving, it is unnecessary to consider their dependence on time. Therefore, it is more convenient to use the complex law of electromagnetic field to discuss the sinusoidal time-varying field.
Remarks
Using different unit systems, the form of Maxwell's equations will be slightly changed, and the general form is still the same, but different constants will appear in different positions within the equation.
The International System of Units is the most commonly used unit system. The entire engineering field uses this unit system. Most chemists also use this unit system. Almost all college physics textbooks use this unit system. System. Other commonly used unit systems are Gauss, Lorentz-Heaviside units and Planck. The Gauss unit system derived from the centimeter-gram-second system is more suitable for teaching purposes and can make equations look simpler and easier to understand. The Lorentz-Heaviside unit system is also derived from the centimeter-gram-second system and is mainly used in particle physics; the Planck unit system is a natural unit system, and its units are defined according to the nature of nature. Set by man. The Planck unit system is a very useful tool for studying theoretical physics and can give great enlightenment. On this page, unless otherwise specified, all equations are in the International System of Units.
Two equivalent expressions of Maxwell’s equations are shown here. The first expression is as follows:
This expression adds the free charge and the bound charge to the total charge required by Gauss's law, and also divides the free current, the bound current and the polarization current The total is the total current in Maxwell-Ampere's law. This expression adopts a relatively basic and micro viewpoint. This expression can be applied to calculate the electric and magnetic fields generated by a finite source charge and a source current in a vacuum. However, in reality, there are too many electrons and atomic nuclei in matter that cannot be included in the calculation. In fact, classical electromagnetism does not need such precise answers.
For the second expression, please refer to the "general form" in the aforementioned "integration form". It takes free charge and free current as the source, and does not directly calculate the contribution of the bound charge appearing in the dielectric and the bound current and the polarization current appearing in the magnetized substance. Since in general actual conditions, the parameters that can be directly controlled are free charge and free current, and bound charge, bound current, and polarization current are phenomena that occur after the substance is polarized. Using this expression will make the dielectric or magnetization Various physical calculations within the substance are easier.
On the surface, Maxwell’s equations seem to be overdetermined. It only has six unknowns (vector electric field and magnetic field each have three unknowns, current and charge are not unknowns. It is a physical quantity that is freely set and conforms to the conservation of charge), but there are eight equations (two Gauss laws have two equations, Faraday’s law and Ampere’s law are vectorial, each containing three equations). This situation is related to the limited repeatability of Maxwell's equations. It can be deduced from the theory that any system that satisfies Faraday's law and Ampere's law must satisfy two Gauss' laws.
On the other hand, Maxwell's equations are not closed. Only given the characteristics of the electromagnetic medium, this system of equations can get a definite solution.
Applicable scale
The Maxwell equations are usually applied to the "macro average field" of various fields. When the scale shrinks to the microscopic scale, so as to approach the size of a single atom, the local fluctuations of these fields will become unignorable, and quantum phenomena will begin to appear. Only under the premise of macro-average, some physical quantities such as the permittivity and permeability of a substance can get meaningful definition values.
The radius of the heaviest nucleus is about 7 femtometers (1fm=10-15m). Therefore, in classical electromagnetics, the microscopic scale refers to the order of magnitude greater than 10-14m. To meet the microscopic scale, electrons and nuclei can be regarded as point charges, and the microscopic Maxwell equations are established; otherwise, the charge distribution inside the nucleus must be taken into consideration. The electric field and magnetic field calculated on the microscopic scale still change quite drastically, the distance of the spatial change is less than 10-10m, and the period of the time change is between 10-17 and 10-13 seconds. Therefore, from the microscopic Maxwell equations, the classical averaging operation must be performed to obtain the smooth, continuous, and slowly changing macroscopic electric field and macroscopic magnetic field. The lowest limit of the macro scale is 10-8 meters. This means that the reflection and refraction behavior of electromagnetic waves can be described by the macro-Maxwell equations. Taking this minimum limit as the side length, a cube with a volume of 10-24 cubic meters contains approximately 106 nuclei and electrons. The physical behavior of so many nuclei and electrons, after classical averaging, is enough to smooth any violent fluctuations. According to reliable literature records, the classical averaging operation only requires averaging in space, not in time, and does not need to consider the quantum effects of atoms.
Significance
Maxwell’s contribution to the creation of the field concept is also a great innovation in physics at that time, because it was the emergence of the field concept that made many physics Scientists were able to get rid of the shackles of Newton's "super-distance concept" and generally accepted the idea that electromagnetic and gravitational effects are both "proximity".
The position of Maxwell's equations in electromagnetics and classical electrodynamics is the same as the position of Newton's laws of motion in Newtonian mechanics. The electromagnetic theory centered on Maxwell's equations is one of the most proud achievements of classical physics. The perfect unity of electromagnetic interaction revealed by it has established a belief for physicists that the various interactions of matter should be unified at a higher level. This theory is widely applied to technical fields.
Scientific significance
(1) The classical field theory was founded by Maxwell in the late 19th century on the basis of summarizing the three experimental laws of electromagnetics and comparing them with mechanical models. But Maxwell’s main achievement precisely enabled him to break out of the constraints of the framework of classical mechanics: in physics, he took "field" instead of "force" as the basic research object, and introduced a vector partial differential operation that is different from classical mathematics in mathematics. Symbol. These two are the basis for the discovery of the electromagnetic wave equation. That is to say, Maxwell's work has actually broken through the framework of classical physics and mathematics at that time, but because of the historical conditions at that time, people can still only understand the electromagnetic field theory from the framework of Newton's calculus and classical mechanics.
Modern mathematics, mathematical analysis in Hilbert space did not appear until the turn of the 19th century and the 20th century. The concept of matter waves in quantum mechanics was discovered at a later time, especially the inseparable mathematical logic connection between modern mathematics and quantum physics has not yet been fully understood and accepted by people. From Maxwell's establishment of electromagnetic field theory to now, people have always used classical mathematics in Euclidean space as the basic method to solve Maxwell's equations.
(2) From the emergence, form, content and historical process of Maxwell’s equations, we can see: First, the physical object develops into a new axiom expression at a deeper level. Being mastered by mankind, scientific progress will not evolve under established premises. The establishment of a new axiom system with cognitive significance is the sign of scientific theoretical progress. Second, although the physical object and the way of expressing it are different things, it is impossible to recognize the "existence" of this object without relying on a proper method of expression. Third, the theory we are building will determine the level of meaning in which we make our objects physical facts. This is exactly the confusion brought to us by modern cutting-edge physics.
(3) Maxwell’s equations reveal the beauty of symmetry in the mutual transformation of electric and magnetic fields. This beauty is fully expressed in modern mathematical form. However, on the one hand, we should admit that only the proper mathematical form can fully demonstrate the integrity (electromagnetic symmetry) that cannot be seen in the empirical method; on the other hand, we should not forget that the beauty of this symmetry is in mathematical form. The unified nature of the electromagnetic field reflected. Therefore, we should realize that we should "discover" or "see" this symmetry in mathematical expressions, rather than directly deducing this essence from physical mathematical formulas.
